广义线性模型(Generalized Linear Model)

广义线性模型(Generalized Linear Model)

本文沿接接着上节的指数分布族,文章中注了引入指数分布族的概念是为了说明广义线性模型。

概念

广义线性模型（generalized linear model, GLM)是简单最小二乘回归（OLS)的扩展,在广义线性模式中，假设每个变量的观测值 $Y$ 来自某个指数族分布。 该分布的平均数 $\mu$ 可由与该点独立的 $X$ 解释： $$E(y)=\mu=g(\theta^Tx)$$

其中$E(y)$为 $y$ 的期望值，$\theta^T x$是由未知待估计参数$\theta$与已知变数 $X$ 构成的线性估计式，$g$ 则为链接函数。 在此模式下,$y$ 的方差 $V$ 可表示为： $$Var(y)=V(y)=V(g(\theta ^Tx))$$ 一般假设 $V$ 可视为一指数族随机变数的函数。未知参数 $\theta$ 通常会以最大似然、贝叶斯方法估计。

例证

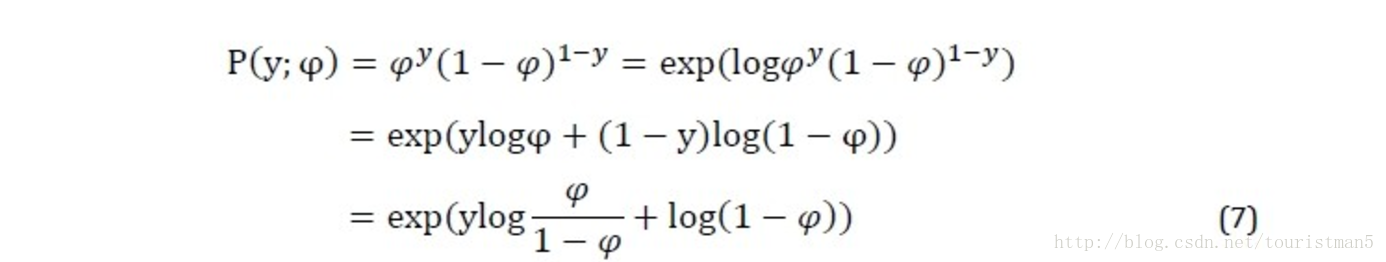
参考此例：$\eta$ 与伯努利分布中的参数 $\varphi$ 的关系是 $\text{Logistic}$ 函数，再通过推导可以得到 $\text{Logistic}$ 回归。见下文推导示例。

通过此例，我们可以推想，$\eta$以不同的映射函数与其他概率分布函数中的参数发生联系，从而得到不同的模型，广义线性模型正是将指数族分布中的所有成员都作为线性模型的扩展，通过非线性的连接函数映射到其他空间从而大大扩大了线性模型可解决的问题。

假设条件

下面我们看看GLM的形式话定义，GLM的三个假设：

1. $y|x;\theta～ExpFamily(\eta)$：给定样本 $x$ 与参数 $\theta$,样本分类 $y$ 服从指数分布族中的某个分布
2. 给定一个 $x$ ，我们需要的目标函数为$h_\theta(x)=E\left[ T(y)|x\right]$
3. $\eta=\theta^Tx$

上例推导

依据三个假设，我们可以推导出logistic模型与最小二乘模型。Logistic模型的推导过程如下： $$h_\theta(x)=E\left[ T(y)|x\right] =E\left[ y|x\right]=\mu=\eta=\theta^Tx$$

其中，将$\eta$与原始概率分布中的参数联系起来的函数成为正则相应函数，如$\varphi=\frac{1}{1+e^(-\eta)},\mu=\eta$即是正则响应函数。正则响应函数的逆称为正则关联函数。

所以，对于广义线性模型，需要决策的是选用什么样的分布，当选取高斯分布时，我们可以得到最小二乘模型，当选取伯努利分布时，我们得到logistic模型，这里所说的模型是假设函数 $h$ 的形式。

同样，可以将Logistic函数做拉伸变换，可以得到新的连接函数

$$\varphi=\frac{1}{1+e^{-\lambda\eta}}$$

总结

总计来说，广义线性模型通过假设一个概率分布函数，得到不同的模型，而之前讨论的梯度下降法、牛顿法都是为了求取线性模型中的线性部分 $(\theta ^Tx)$ 的参数 $\theta$ 的。

GLM是NLM的直接推官，它不仅可以用于连续数据，更重要的是或它的根本价值在于可用于离散数据。 其中1983年，P.McCullagh & J.A.Nelder合著世界上第一本GLM的专著。

参考链接：

1. https://zh.wikipedia.org/wiki/廣義線性模型
2. http://blog.csdn.net/stdcoutzyx/article/details/9207047
3. 张尧庭(1995). 线性模型与广义线性模型